Varför delar vi inte med noll?
Läsare kanske undrar varför jag ägnar en hel artikel åt en så trivial fråga? Anledningen är det häpnadsväckande antalet studenter (!) som slarvigt genomför den kallade operationen. Och inte bara studenter. Ibland fångar jag lärare också. Vad kan elever till sådana lärare göra i matematik? Den omedelbara anledningen till att skriva denna text var ett samtal med en lärare för vilken division med noll inte var något problem...
Med noll, ja, ingenting alls förutom krångel, eftersom vi egentligen inte behöver använda det i vardagen. Vi går inte till affären för noll ägg. "Det finns en person i rummet" låter på något sätt naturligt, men "noll personer" låter konstlat. Språkvetare säger att noll är utanför språksystemet.
Vi kan klara oss utan nollan på bankkonton också: använd bara - som på en termometer - röd och blå för positiva och negativa värden (observera att för temperatur är det naturligt att använda rött för positiva tal, och för bankkonton det är tvärtom, eftersom debiteringen bör utlösa en varning, så rött rekommenderas starkt).
Genom att ta med noll som ett naturligt tal berör vi problemet med differentiering grundtal od hushåll. Inom 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …..
talets makt sammanfaller med numret på den plats på vilken den står. Annars finns den redan i sekvensen 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ….
Antalet singleton-set kommer på andra plats, antalet set med två element kommer på tredje plats, och så vidare. Vi måste förklara varför vi till exempel inte numrerar idrottarnas platser i tävlingar från grunden. Då skulle förstaplatsen få en silvermedalj (guld gick till nollplaceringsvinnaren), och så vidare. En något liknande procedur användes i fotboll - jag vet inte om läsarna vet att "liga ett" betyder " följer de bästa." ", och nollligan kallas för att bli "storligan".
Ibland hör vi argumentet att vi måste börja om från början, eftersom det är bekvämt för IT-folk. För att fortsätta med dessa överväganden bör definitionen av en kilometer ändras - den borde vara 1024 m, eftersom detta är antalet byte i en kilobyte (jag kommer att referera till ett skämt känt för datavetare: "Vad är skillnaden mellan en nybörjare och en student i datavetenskap och en femteårsstudent vid denna fakultet? att en kilobyte är 1000 kilobyte, den sista - att en kilometer är 1024 meter")!
En annan punkt som redan bör tas på allvar är denna: vi mäter alltid från grunden! Titta bara på vilken våg som helst på en linjal, på hushållsvåg, till och med på en klocka. Eftersom vi mäter från noll, och räkning kan förstås som ett mått med en dimensionslös enhet, bör vi räkna från noll.
Det är en enkel sak, men...
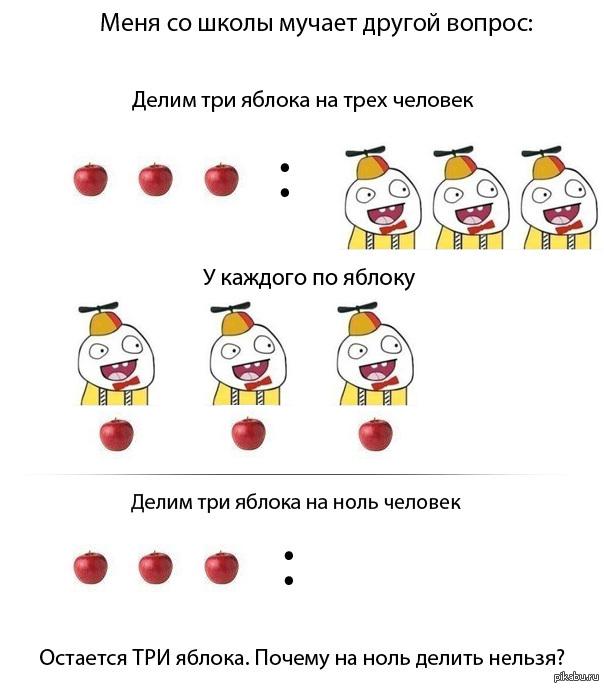
Låt oss lämna det allmänna resonemanget och återgå till division med noll. Saken är enkel och det skulle vara enkelt om det inte vore för ... så vad? Låt oss tänka och försöka. Hur mycket kan det bli - en dividerad med noll? Låt oss se: 1/0 = x. Multiplicera båda sidor med nämnaren på vänster sida.
Vi får 1=0. Är det något fel! Vad har hänt? Ah, en gissning! Antagandet att det finns en kvot på ett och noll leder till en motsägelse. Och om ett tal inte kan delas med noll, kan ett annat tal delas. Om du, läsare, rycker på axlarna och undrar varför författaren (det vill säga jag) skriver om sådana banaliteter, då... Jag är mycket glad!
Formeln 0/0 = 0 skulle kunna argumenteras envist, men den motsäger regeln att resultatet av att dividera ett tal med sig självt är lika med ett. Helt men helt olika är symboler som 0/0, °/° och liknande i matematisk analys. De betyder inte vilket nummer som helst, utan är en symbolisk beteckning på särskilda sekvenser av vissa typer.
Jag hittade en intressant jämförelse i en elektroteknikbok: att dividera med noll är lika farligt som högspänningselektricitet. Detta är normalt: Ohms lag säger att förhållandet mellan spänning och resistans är lika med ström: V = U/R. Om motståndet var noll, skulle en teoretiskt oändlig mängd ström flyta genom ledaren och bränna upp alla möjliga ledare.
Jag skrev en gång en dikt om farorna med nolldelning – för alla dagar i veckan. Jag minns att den mest dramatiska dagen var torsdagen, men jag tycker synd om allt mitt arbete på det här området.
När du dividerar något med noll
Väldigt tidig måndag
Veckan som precis hände
Du är redan helt misslyckad.
När på tisdag eftermiddag
Du sätter en nolla i nämnaren
Jag ska säga dig då, du har fel
Min dåliga matematiker!
När genom noll, genom perversitet,
Vill du dela på onsdag?
Du kommer att hamna i mycket problem
Du har hö och vatten i huvudet!
En viss Bartek var med oss.
Han var oförenlig med reglerna.
På torsdag delas det med noll.
Han är inte längre mellan oss!
Om en konstig önskan tar över dig,
Dividera med noll på fredag
Jag ska säga det rakt av ärligt:
Dålig start på helgen.
När den når noll, någon gång på lördag
Avdelaren blir din (inte fetstil)
Knäböj under kyrkstaketet.
Detta är din söndagsomvändelse.
Vill du ha en nolla under strecket?
Bestäm semestern på söndag
Ta med krita, svart tavla.
Skriv: det är inte delbart med noll!
Noll är förknippat med tomhet och ingenting. Faktum är att det kom till matematik som en kvantitet som, när den läggs till något värde, inte ändrar det: x + 0 = x. Men nu förekommer noll i flera andra betydelser, framför allt som skalans början. Om det varken är positiv temperatur eller frost utanför fönstret, då ... det här är noll, vilket inte betyder att det inte finns någon temperatur alls. Ett nollklassmonument är inte ett som har rivits på länge och helt enkelt inte existerar. Tvärtom är det något som Wawel, Eiffeltornet och Frihetsgudinnan.
Nåväl, vikten av noll i ett positionssystem kan inte överskattas. Vet du, läsare, hur många nollor Bill Gates har på sitt bankkonto? Jag vet inte, men jag vill ha hälften. Tydligen märkte Napoleon Bonaparte att människor är som nollor: de får mening genom position. I Andrzej Wajdas film As the Years, As the Days Pass exploderar den passionerade konstnären Jerzy: "Filistin är noll, nihil, ingenting, ingenting, nihil, noll." Men noll kan vara bra: ”noll avvikelse från normen” betyder att allt går bra, och behåll det så!
Låt oss återgå till matematiken. Noll kan ostraffat adderas, subtraheras och multipliceras. "Jag gick upp noll kilo", säger Manya till Anya. "Och det är intressant, för jag gick ner i samma vikt", svarar Anya. Så låt oss äta sex noll portioner glass sex gånger, det kommer inte att skada oss.
Vi kan inte dividera med noll, men vi kan dividera med noll. En tallrik med noll dumplings kan lätt skickas runt till de som väntar på mat. Hur mycket får varje person?
Noll är inte positivt eller negativt. Detta är numret icke-positivaи icke-negativ. Den uppfyller ojämlikheterna x≥0 och x≤0. Motsägelsen "något positivt" är inte "något negativt", utan "något negativt eller lika med noll". Matematiker, i motsats till språkets regler, kommer alltid att säga att något är "noll" snarare än "noll". För att motivera denna praxis har vi: om vi läser formeln x = 0 "x är lika med noll", då x = 1 läser vi "x är lika med ett", vilket skulle kunna sväljas, men hur är det med "x = 1534267"? Du kan inte heller tilldela ett numeriskt värde till tecknet 00inte heller höja noll till en negativ potens. Å andra sidan kan du rota noll efter behag... och resultatet blir alltid noll,
Exponentialfunktion y = ax, den positiva basen av a, blir aldrig noll. Det följer att det inte finns någon nolllogaritm. Faktum är att logaritmen för a till bas b är en exponent till vilken basen måste höjas för att få logaritmen för a. När a = 0 finns ingen sådan indikator, och noll kan inte vara basen för logaritmen. Nollan i "nämnaren" för Newtons symbol är dock något annat. Vi utgår från att dessa avtal inte leder till motsägelse.
Falska bevis
Division med noll är ett vanligt tema för falska bevis, och det händer även för erfarna matematiker. Låt mig ge er två av mina favoritexempel. Den första är algebraisk. Jag ska "bevisa" att alla siffror är lika. Anta att det finns två tal som inte är lika. Därför är en av dem större än den andra, låt a > b. Låt oss anta att c är deras skillnad
c \uXNUMXd a - b. Så vi har a - b = c, varav a = b + c.
Vi multiplicerar båda delarna av den senare med a - b:
a2 – ab = ab + ac – b2 – bc.
Jag flyttar ak till vänster sida, naturligtvis minns jag om bytet av tecken:
a2 – ab – ac = ab – b2 – bc.
Jag utesluter vanliga faktorer:
A(a-b-c) = b(a-b-c),
Jag delar och jag har det jag ville ha:
a = b.
Och faktiskt ännu märkligare, eftersom jag antog att a > b, och jag fick att a = b. Medan i exemplet ovan är "fusket" lätt att känna igen, i det geometriska beviset nedan är det inte så lätt. Jag ska bevisa att... trapetsen inte existerar. Figuren som vanligtvis kallas trapets existerar inte.
Men låt oss först anta att det finns något sådant som en trapets (ABCD i figuren nedan). Den har två parallella sidor ("baser"). Låt oss utöka dessa baser, som visas på bilden, så att vi får ett parallellogram. Dess diagonaler delar upp trapetsens andra diagonal i segment vars längder betecknas x, y, z, som i bild 1. Från likheten mellan motsvarande trianglar får vi proportionerna:
varifrån vi bestämmer:
Oraz
varifrån vi bestämmer:
Subtrahera sidorna av likheten markerade med asterisker:
Om vi förkortar båda sidorna med x − z får vi – a/b = 1, vilket betyder att a + b = 0. Men talen a, b är längden på trapetsens baser. Om deras summa är noll, så är de också noll. Det betyder att en figur som en trapets kan inte existera! Och eftersom rektanglar, romber och kvadrater också är trapetser, så, kära läsare, finns det inga romber, rektanglar och kvadrater heller ...
Sådär
Att dela är den mest intressanta och utmanande av de fyra grundläggande aktiviteterna. Här möter vi för första gången fenomenet som är så vanligt i vuxen ålder: "gissa svaret och kolla sedan om du gissade rätt." Daniel K. Dennett uttryckte det mycket exakt ("How to Make Mistakes?", i How It Is - A Scientific Guide to the Universe, CiS, Warszawa, 1997):
Denna metod att "gissa" stör inte våra mogna liv - kanske för att vi lär oss det tidigt och att gissa är inte svårt. Ideologiskt förekommer samma fenomen till exempel vid matematisk (fullständig) induktion. Där ”gissar” vi formeln och kontrollerar sedan om vår gissning stämmer. Eleverna frågar alltid: ”Hur skulle vi veta mönstret? Hur kan jag få ut det?" När elever ställer den här frågan till mig förvandlar jag deras fråga till ett skämt: "Jag vet det här för att jag är en professionell, för jag får betalt för att veta det här." Elever i skolan kan besvaras i samma stil, bara mer seriöst.
övning. Observera att vi börjar addition och skriftlig multiplikation med en enhet av lägre ordning och division med en enhet av högre ordning.
Kombination av två idéer
Mattelärare har alltid påpekat att det vi kallar splittring i vuxen ålder är föreningen av två begreppsmässigt olika idéer: hölje i separation.
Den första av dem (hölje) förekommer i problem där arketypen är:
Dela-dela det här är uppgifter som:
? (Vi behåller den ursprungliga stilen för detta problem, hämtat från Julian Zgozalewiczs handbok som publicerades i Krakow 1892 - złoty är den rheniska złoty, valutan som var i omlopp i det österrikisk-ungerska riket fram till början av XNUMX-talet).
Tänk nu på två problem med den äldsta matematikläroboken på polska, fader Tomasz Klos (1538). Är detta en division eller en coupé? Lös det som det anstår skolbarn på XNUMX-talet:
(Polsk till polsk översättning: Det finns en quart och fyra krukor i en tunna. En kruka är fyra quarts. Någon köpte 20 tunnor vin för 50 zł för handel. Tull och skatt (excis?) blir 8 zł. Hur mycket sälja en liter för att tjäna 8 zł?)
Sport, fysik, kongruens
Ibland inom sport måste man dividera något med noll (målkvot). Nåväl, domarna hanterar det på något sätt. Men i abstrakt algebra står de på agendan. kvantiteter som inte är nollvars kvadrat är noll. Detta kan till och med förklaras enkelt.
Betrakta en funktion F som tilldelar en punkt (y, 0) till en punkt på planet (x, y). Vad är F2, det vill säga en dubbel exekvering av F? Nollfunktion - varje punkt har en bild (0,0).
Slutligen, kvantiteter som inte är noll vars kvadrat är 0 är nästan dagligt bröd för fysiker, och tal av formen a + bε, där ε ≠ 0, men ε2 = 0, kallar matematiker dubbla siffror. De finns i matematisk analys och differentialgeometri.
Det finns trots allt något inom aritmetiken som har division med noll åtminstone i namnet. Detta kommer från kongruens. Låt Z beteckna mängden heltal. Att dividera mängden Z med p innebär att vi likställer varje tal (heltal) med några andra, nämligen med de som deras skillnad är delbar med. Så, när vi har fem typer av tal som motsvarar talen 0, 1, 2, 3, 4 - de möjliga resterna när de divideras med 5. Formeln skrivs så här:
mod när skillnaden är en multipel.
Vid = 2 har vi bara två tal: 0 och 1. Att dela heltal i två sådana klasser motsvarar att dela upp dem i jämna och udda. Vi byter ut den nu. Skillnaden är alltid delbar med 1 (vilket heltal som helst är delbart med 1). Kan vi ta =0? Låt oss försöka: när är skillnaden mellan två tal en multipel av noll? Endast när dessa två siffror är lika. Så att dividera en uppsättning heltal med noll är vettigt, men det är inte kul: ingenting händer. Det bör dock understrykas att det inte är fråga om taldelning i den mening som är känd från folkskolan.
Sådana handlingar är helt enkelt förbjudna, liksom lång och bred matematik.
Ris. 2. Identifiera nummer med hjälp av jämförelse
(träd 5 och träd 2)

